Serie numeriche – Ragionamento numerico

Tra le tipologie di quiz di logica maggiormente presenti nell’ambito dei concorsi pubblici , vi sono le serie numeriche, chiamate anche nell’ambito della Logica FOMEZ/RIPAM quiz di ragionamento numerico.

Le serie numeriche rientrano nella sottocategoria dei quiz di logica numerica, ossia di quei quiz di logica per la cui soluzione è necessario individuare un legame numerico tra gli elementi di varia natura contenuti nella domanda (numeri, simboli grafo/numerici, strutture grafo/numeriche, etc.).

Interrogando il nostro database (4.000.000 di quiz), abbiamo sintetizzato in questa voce del nostro glossario le tipologie di serie numeriche che di regola sono oggetto di domanda nell’ambito delle prove concorsuali.

Terminata la lettura potrai esercitarti sull’argomento accedendo al Simulatore Quiz di Concorsando.it ed aggiungendo alla tua area di studio il percorso formativo “Logica numerica”.

Se hai la necessità di studiare in maniera approfondita l’argomento, nonché le altre tipologie di quiz di logica, ti consigliamo di iscriverti al nostro corso online per imparare a risolvere i quiz di logica nei concorsi pubblici.

Ti ricordiamo che acquistando il suddetto corso avrai accesso anche al Corso online di Logica Formez.

Serie numeriche – Le tipologie che incontri nei concorsi pubblici

Nozioni iniziali

Per serie numerica si intende una successione finita ed ordinata di numeri (o termini), costruita in base ad una determinata logica.

Per “logica” si intende l’algoritmo di calcolo, contenente una o più operazioni matematiche, mediante il quale vengono costruiti i termini della serie.

Di regola le tipologie di operazioni che potenzialmente possono essere utilizzate, anche contestualmente, all’interno di una logica sono le seguenti:

• addizione;
• sottrazione;
• moltiplicazione;
• divisone;
• elevazione a potenza;
• estrazione di radice quadrata.

Nei quiz aventi ad oggetto serie numeriche il candidato, per individuare la risposta giusta, e dunque il termine o i termini mancanti della serie, deve necessariamente dedurne la logica di costruzione analizzando da sinistra verso destra le relazioni che intercorrono tra i termini noti.

Di seguito, per comodità didattica, rappresenteremo i termini delle serie numeriche con le lettere (in maiuscolo) dell’alfabeto (A B C D E F) oppure specificando (da sinistra verso destra) la loro posizione (primo termine, secondo termine, terzo termine, etc.).

Logiche cicliche

La logica è ciclica se contiene una o più operazioni matematiche che si ripetono ciclicamente.

Ad esempio dato come 2 il primo termine della serie, una serie con logica +2 ·3 sarà in tal modo strutturata

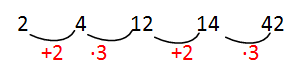
B = A +2    C = B · 3    D = C +2    E = D · 3

Volendo esprimere la logica a parole: per ottenere il secondo termine aggiungi due al primo, per ottenere il terzo termine moltiplica per tre il secondo termine e così via.

Logiche cicliche con una sola operazione

Le logiche cicliche più semplici sono quelle che utilizzano un’unica tipologia di operazione.

Ad esempio la logica può essere ·2 (per due)

B = 2 ·A    C = 2 ·B    D =2 ·C    E = 2·D

Generalizzando potremmo scrivere che le logiche sequenziali con un’unica tipologia di operazione si comportano in questo modo:

B = [operazione] A    C = [operazione] B   D =[operazione] C
E = [operazione] D

Di seguito alcuni esempi di quiz in cui le serie numeriche utilizzano logiche cicliche con un’unica operazione. Nei quiz successivi la risposta giusta è sempre la prima

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
10 20 ? 80	40	60	30	50	·2
? 12 36 108	4	6	3	2	·3
3 9 ? 81 243	27	25	29	33	·3
0,5 ? 8 32 128	2	1	1.5	2.5	·4
2 12 ? 432	72	144	24	112	·6
120 60 ? 15	30	45	20	50	:2
0,7 ? 1,7 2,2 2,7	1.2	1.5	1.6	2	+0,5
? 34 45 56	23	72	33	29	+11
? 54 65 76 87	43	33	30	41	+11
? 61 79 97 115	43	40	26	30	+18
? 58 60 62	56	52	45	35	+2
1 4 ? 10	7	5	6	3	+3
? 22 29 36	15	10	19	13	+7
? 24 31 38	17	20	19	15	+7
? 31 39 47	23	29	27	25	+8
? 41 49 57	33	29	24	37	+8
? 53 61 69	45	39	40	51	+8
? 12 11 10	13	15	9	16	-1
? 33 29 25	37	39	47	40	-4
? 33 27 21	39	37	36	43	-6

Logiche cicliche con due o più operazioni

Le logiche cicliche possono anche contemplare due operazioni matematiche.

Ad esempio dato come 2 il primo termine della serie, una serie con logica -2 ·4 sarà in tal modo strutturata:

B = A-2    C =B·4    D =C-2    E = D·4

Generalizzando potremmo scrivere che le logiche sequenziali con due operazioni si comportano in questo modo:

B = [operazione_1] A    C = [operazione_2] B   D =[operazione_1] C  
E = [operazione_2] D

Si evidenzia che alcune logiche possono utilizzare a loro interno anche più di due operazioni: ad esempio la logica potrebbe essere +2, +1, -5.

B = A+2    C =B+1    D =C-5    E = D+2    F = E+1    G= F-5 

Di seguito alcuni esempi di quiz in cui le serie numeriche utilizzano logiche cicliche con due operazioni. Nei quiz successivi la risposta giusta è sempre la prima.

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
13 13 26 26 ?	52	60	33	32	·1·2
? 36 18 18 9	36	72	38	48	·1:2
33 66 ? 132 132	66	70	71	63	·2·1
5 10 30 60 ?	180	360	100	150	·2·3
? 24 23 46 45	12	10	16	27	·2-1
11 22 ? 30 23	15	44	33	18	·2-7
1 ? 18 54 324	3	9	2	16	·3·6
3 9 10 ? 31	30	32	28	25	·3+1
3 9 ? 36 39	12	24	18	10	·3+3
3 9 ? 45 51	15	27	18	30	·3+6
20 60 40 120 ?	100	90	120	70	·3-20
20 80 ? 340 345	85	320	160	75	·4+5
3 12 ? 44 43	11	9	24	15	·4-1
? 30 90 450 1350	6	60	15	17	·5·3
? 5 15 75 225	1	2	8	10	·5·3
1 5 ? 60 67	12	10	25	3	·5+7
? 20 11 55 46	4	2	5	12	·5-9
2 14 ? 196 392	28	42	17	16	·7·2
2 1 ? 2 8	4	5	7	1	:2·2
50 25 ? 50 200	100	105	125	150	:2·4
? 90 30 15 5	180	100	208	80	:2:3
200 100 ? 10 2	20	80	70	15	:2:5
100 50 10 5 ?	1	7	15	3	:2:5
? 4 10 5 11	8	7	15	6	:2+6
500 ? 200 100 50	250	220	200	100	:2-50
? 84 42 14 7	252	210	336	168	:3:2
100 25 24 ? 5	6	8	10	20	:4-1
4000 800 ? 40 10	200	100	125	25	:5:4
150 30 35 ? 12	7	8	9	10	:5+5
12 23 ? 37 40	26	24	20	31	+11+3
? 25 50 52 104	23	21	20	22	+2·2
? 90 100 120 130	70	80	75	85	+20+10
1 4 ? 10	7	5	6	3	+3
13 17 ? 11 1	7	5	19	14	+4-10
? 15 9 13 7	11	14	8	10	+4-6
10 14 7 ? 4	11	6	8	3	+4-7
5 10 ? 17 19	12	13	16	11	+5+2
? 20 27 33 40	14	12	15	7	+6+7
? 10 20 27 54	3	2	8	4	+7·2
2 9 ? 34 102	27	25	29	33	+7·3
2 9 ? 15 14	8	13	11	6	+7-1
2 11 22 ? 42	31	44	34	66	+9+11
? 12 7 16 11	3	2	10	7	+9-5
10 9 18 17 ?	34	32	30	28	-1·2
? 46 40 29 23	57	48	60	53	-11-6
? 15 12 11 8	16	20	22	17	-1-3
10 8 14 12 18 ?	16	8	21	15	-2+6
? 6 7 4 1 2	9	5	15	14	-3+1
12 8 24 ? 36	20	24	30	14	-4+16
? 12 20 15 23	17	22	25	16	-5+8
20 ? 15 7 10	12	19	14	22	-8+3
? 24 31 40 47	15	30	10	5	9+7

Logiche progressive

Le logiche progressive si caratterizzano per l’utilizzo in maniera progressiva di un’unica tipologia di operazione.

Un esempio di logica progressiva può essere +2+4+6+8. Qui come vedete l’operazione è sempre la stessa, ma l’addendo, ossia il numero da aggiungere, aumenta sempre più, via via che ci spostiamo verso destra:

B = A+2    C =B+4    D =C+6   E = D+8

Nell’esempio la logica prevede che il secondo termine si ottenga aggiungendo 2 al primo, il terzo termine si ottenga aggiungendo 4 al secondo, il quarto termine si ottenga aggiungendo 6 al terzo ed infine il quarto termine si ottenga aggiungendo 8 al terzo.

In altri termini nelle logiche progressive si utilizza un’unica operazione che ad ogni passaggio (dal primo al secondo, dal secondo al terzo termine, e così via) cambia il “fattore” di calcolo.

La progressione può essere crescente (es. ·1·2·3·4·5·6) o decrescente (es. :5:4:3:2:1)

Di seguito alcuni esempi di quiz in cui le serie numeriche utilizzano logiche progressive crescenti. Nei quiz successivi la risposta giusta è sempre la prima.

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
1 1 2 6 ?	24	20	18	28	·1·2·3·4
13 13 26 78 ?	312	302	322	332	·1·2·3·4
1 1 3 ? 105	15	9	12	24	·1·3·5·7
? 180 60 15 3	360	60	120	540	:2:3:4:5
? 6 8 12 20	5	1	3	7	+1+2+4+8
? 10 14 22 38	8	12	5	4	+2 +4 +8 +16
? 34 38 43	31	27	30	28	+3+4+5
? 85 89 94 100	82	78	80	75	+3+4+5+6
2, 5, 11, ?, 47	23	22	17	25	+3+6+12+24
2 7 17 37 ?	77	72	74	63	+5+10+20+40
? 100 112 130 154	94	95	90	88	+6 +12 +18 +24
2 8 ? 23 32 42	15	11	10	21	+6+7+8+9+10
113 100 74 ?	35	30	75	70	-13-26-39
10 8 5 ?	1	2	4	3	-2-3-4
? 37 34 30 25	39	40	41	42	-2-3-4-5
28 ? 21 13 2	26	27	25	22	-2-5-8-11
93 90 85 ? 69	78	81	83	85	-3-5-7-9

Di seguito alcuni esempi di quiz in cui le serie numeriche utilizzano logiche progressive decrescenti. Nei quiz successivi la risposta giusta è sempre la prima.

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
1 ? 10 13 15	6	5	7	9	+5+4+3+2
1 ? 20 60 120	5	8	4	15	·5·4·3·2
100 104 ? 109 110	107	103	100	101	+4+3+2+1
2 7 11 ?	14	15	18	13	+5+4+3
? 16 9 4	25	20	10	6	-9-7-5
3 9 13 15 ?	15	13	14	16	+6+4+2+0
? 12 4 2 2	48	96	36	60	:4:3:2:1
? 12 9 7	16	22	14	18	-4-3-2
? 134 130 127 125	139	137	136	141	-5-4-3-2

Logiche a coppie

Esistono poi delle serie numeriche dove la logica non si applica a tutti termini bensì sulle singole coppie di termini di cui la serie si compone (c.d. logiche a coppie).

A B | C D | E F

In altri termini nella fattispecie la serie numerica viene divisa in due o più coppie di termini e all’interno di ognuna di esse trova applicazione la logica individuata.

È ovvio che solo le serie numeriche con un numero pari di termini possono presentare delle logiche a coppie.

Ora andremo ad elencare le varie tipologie di logiche a coppie che possiamo incontrare nelle banche dati. Precisiamo che negli esempi successivi per comodità didattica faremo riferimento sempre alla prima coppia |A B| per indicare la logica che si applica a tutte le coppie della serie.

La logica B = A + NUMERO

La prima tipologia di logica a coppie che possiamo incontrare nei quiz è la seguente

B = A + NUMERO

In pratica qui per ottenere il secondo termine della coppia aggiungiamo un certo numero al primo.

Ad esempio svolgiamo questo quiz.

dividiamo la serie in coppie

11  14 | ?  2 | 17   8

in questo caso come appare chiaro nella prima e terza coppia la somma dei termini da sempre 25. Dunque la risposta giusta  è E) ossia 23

11 + 14 = 25 | 23 + 2= 25 | 17 + 8 = 25

È chiaro che questa logica può essere generalizzata in modo da comprendere le altre operazioni

B = A [operazione] NUMERO

Quindi potremmo avere anche:

B = A – NUMERO

B = A · NUMERO

B = A : NUMERO

Di seguito alcuni esempi di quiz in cui le serie numeriche utilizzano le logiche a coppie appena analizzate. Nei quiz successivi la risposta giusta è sempre la prima.

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
1 1 1 5 ? 125	25	7	15	11	B = A ·5
? 21 39 50 24 35	10	5	14	12	B = A+11
10, 30, 17, 51, 38, 114, ?, ?	101, 303	101, 293	111, 303	100, 202	B=A·3
10, 30, 18, 54, 42, 126, ?, ?	114, 342	114, 332	124, 342	113, 228	B=A·3
10, 30, 19, 57, 46, 138, ?, ?	127, 381	127, 371	137, 381	126, 254	B=A·3
11, 33, 20, 60, 47, 141, ?, ?	128, 384	128, 374	138, 384	127, 256	B=A·3
11, 33, 21, 63, 51, 153, ?, ?	141, 423	141, 413	151, 423	140, 282	B=A·3
11, 33, 22, 66, 55, 165, ?, ?	154, 462	154, 452	164, 462	153, 308	B=A·3
12, 36, 23, 69, 56, 168, ?, ?	155, 465	155, 455	165, 465	154, 310	B=A·3
12, 36, 24, 72, 60, 180, ?, ?	168, 504	168, 494	178, 504	167, 336	B=A·3
12, 36, 25, 75, 64, 192, ?, ?	181, 543	181, 533	191, 543	180, 362	B=A·3
13, 39, 26, 78, 65, 195, ?, ?	182, 546	182, 536	192, 546	181, 364	B=A·3
13, 39, 27, 81, 69, 207, ?, ?	195, 585	195, 575	205, 585	194, 390	B=A·3
9, 27, 14, 42, 29, 87, ?, ?	74, 222	74, 212	84, 222	73, 148	B=A·3
9, 27, 15, 45, 33, 99, ?, ?	87, 261	87, 251	97, 261	86, 174	B=A·3
9, 27, 16, 48, 37, 111, ?, ?	100, 300	100, 290	110, 300	99, 200	B=A·3
1 ? 11 66 8 48	6	12	9	4	B=A·6
10 90 ? 45 6 54	5	7	9	3	B=A·9
100 10 20 2 350 ?	35	3	50	150	B=A:10
157 155 206 ? 87 85	204	169	309	75	B=A-2

La logica A + B  = NUMERO

Un’altra delle logiche a coppie che maggiormente possiamo incontrare è la seguente

A + B = NUMERO

In pratica dunque la serie numerica è strutturata in coppie di termini, e in ogni coppia la somma dei termini da sempre lo stesso valore.

La logica appena vista può essere generalizzata in modo da comprendere anche la altre tipologie di operazioni

A [OPERAZIONE] B = NUMERO

In particolare possiamo avere che i termini di ogni coppia siano i termini:

• di una moltiplicazione: A · B = NUMERO
• di una divisione: A : B = NUMERO;
• di un addizione A + B = NUMERO;
• di una sottrazione A – B = NUMERO.

Di seguito alcuni esempi di quiz in cui le serie numeriche sono costruite in base alle logiche a coppie appena analizzate

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
1 ? 10 10 12 8	19	22	20	14	A+B=20
? 27 14 14 6 22	1	11	27	29	A + B = 28

La logica A = B²

Un’altra tipologia di logica a coppie che spesso si può incontrare nei quiz di ragionamento numerico è la seguente:

A = B² 

Qui dunque il primo termine rappresenta il quadrato del secondo, ossia il secondo termine rappresenta la radice quadrata del primo termine

B = √A

Possiamo avere anche che il secondo sia il quadrato del primo termine

B = A² 

Possiamo anche avere casi i cui un termine sia il cubo dell’altro

A = B³ 

B = A³ 

Di seguito alcune serie numeriche costruite in base alle logiche a coppie appena analizzate

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
? 1 2 4 9 81	1	8	3	5	B = A²
? 4 3 9 5 25	2	7	8	13	B = A²

Logiche a terzine

Esistono poi delle logiche che operano su terzine di termini.

A B C | D E F

E’ chiaro che in questo caso la serie non può che essere formata da un numero di termini uguali o multiplo di tre. Di regola presenta 6 termini.

Anche qui precisiamo che negli esempi successivi per comodità didattica faremo riferimento sempre alla prima terzina |A B C| per indicare la logica che si applica a tutte le terzine della serie.

Di seguito alcune serie numeriche costruite in base a logiche a terzine.

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
? 15 60 21 4 84	4	5	6	34	A·B = C
1 ? 2 8 3 27	1	10	0	5	C = (A·B)+B
1 ? 2 8 4 64	1	20	60	40	C = (A·B)·2
100 ? 4 6 3 2	25	20	15	17	A = B·C
5, 10, 12 . 13, 26, 28 . 29, ?, ?	58, 60	59, 61	57, 59	61, 63	B = A·2  C = B+2
6, 12, 14 . 15, 30, 32 . 33, ?, ?	66, 68	67, 69	65, 67	70, 72	B = A·2  C = B+2

Logiche alternate

Le logiche alternate contemplano due tipologie di operazioni di cui una si applica ai termini in posizione dispari e l’altra ai termini in posizioni pari

Facciamo subito un esempio per capirci meglio. Analizziamo la seguente serie numerica

2 2 4 4 6 8

Questa serie segue la seguente logica alternata +2 ∙2

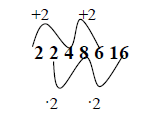
In particolare:

• l’operazione +2 si applica in maniera sequenziale al I, III e V termine;
• l’operazione ∙2 si applica in maniera sequenziale al II, IV, VI termine.

Di seguito alcune serie numeriche costruite in base a logiche alternate.

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
11 75 33 71 ? 67	99	60	70	39	·3-4
? 4 18 32 9 256	36	64	72	48	:2 ·8
? 13 7 11 8 9	6	12	10	4	+1 -2
1 4 2 5 3 ?	6	7	8	9	+1+1
68, 66, 69, 65, 70, 64, 71, ?	63	80	69	86	+1-1
?, ?, 10, 61, 15, 64, 20, 67	5, 58	58, 5	3, 58	7, 58	+5+3
?, ?, 11, 60, 16, 63, 21, 66	6, 57	57, 6	4, 57	8, 57	+5+3
?, ?, 12, 59, 17, 62, 22, 65	7, 56	56, 7	5, 56	9, 56	+5+3
?, ?, 13, 58, 18, 61, 23, 64	8, 55	55, 8	6, 55	10, 55	+5+3
?, ?, 14, 57, 19, 60, 24, 63	9, 54	54, 9	7, 54	11, 54	+5+3
?, ?, 16, 55, 21, 58, 26, 61	11, 52	52, 11	9, 52	13, 52	+5+3
?, ?, 17, 54, 22, 57, 27, 60	12, 51	51, 12	10, 51	14, 51	+5+3
?, ?, 18, 53, 23, 56, 28, 59	13, 50	50, 13	11, 50	15, 50	+5+3
?, ?, 19, 52, 24, 55, 29, 58	14, 49	49, 14	12, 49	16, 49	+5+3
?, ?, 21, 50, 26, 53, 31, 56	16, 47	47, 16	14, 47	18, 47	+5+3
?, ?, 22, 49, 27, 52, 32, 55	17, 46	46, 17	15, 46	19, 46	+5+3
?, ?, 23, 48, 28, 51, 33, 54	18, 45	45, 18	16, 45	20, 45	+5+3
?, ?, 24, 47, 29, 50, 34, 53	19, 44	44, 19	17, 44	21, 44	+5+3
?, ?, 25, 46, 30, 49, 35, 52	20, 43	43, 20	18, 43	22, 43	+5+3
?, ?, 8, 63, 13, 66, 18, 69	3, 60	60, 3	1, 60	5, 60	+5+3
?, ?, 9, 62, 14, 65, 19, 68	4, 59	59, 4	2, 59	6, 59	+5+3
20 ? 14 20 8 11	29	32	27	23	-6-9

Logiche a cifre 

Ci sono anche delle logiche in cui si prendono i considerazione le cifre di cui si compongono i vari numeri contenuti nella serie.

Ad esempio nel quiz

81 63 53 27 ?

A) 90        B) 33          C) 8      D) 17

La risposta giusta è A (ossia 90) in quanto la somma delle cifre di cui si compone ogni termine è uguale sempre a 9.

Logiche complesse

Infine esistono delle logiche complesse in cui il terzo termine è il risultato di un’operazione tra il primo ed il secondo ed il quinto termine è il risultato di un’operazione tra il terzo e il quarto.

A [OPERAZIONE] B = C   C [OPERAZIONE] D = E

Di seguito alcune serie numeriche costruite in base a logiche complesse.

Domanda	Risposta 1	Risposta 2	Risposta 3	Risposta 4	Logica
? 34 22 12 10	56	48	51	68	A-B=C   C-D=E
? 6 17 8 25	11	16	23	18	A+B=C  C+D=E
? 7 16 3 13	23	14	10	21	A-B=C   C-D=E

Successione di Fibonacci

Una particolare logica complessa è la successione di Fibonacci, che consiste in una successione di numeri interi positivi in cui ciascun numero è la somma dei due precedenti e i primi due termini della successione sono per definizione uguali a 1.

A = 1    B = 1    C = A + B    D = C + B    E = D + C 

I primi termini della successione di Fibonacci sono: 1, 1, 2, 3 5, 8, 13, 21, 34, 55, 89, 144, …